Page 298 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

5. BÖLÜM ÇOKGENLER - II

Soru:
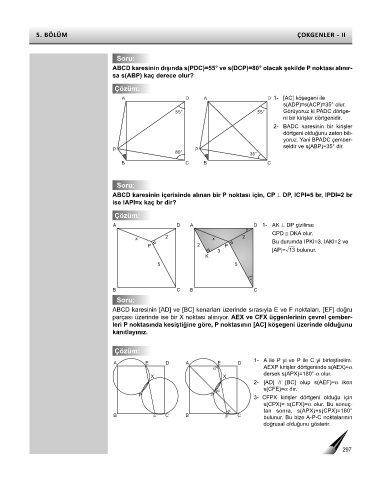
ABCD karesinin dışında s(PDC)=55° ve s(DCP)=80° olacak şekilde P noktası alınır-
sa s(ABP) kaç derece olur?
Çözüm:
A D A D 1- [AC] köşegeni ile
s(ADP)=s(ACP)=35° olur.
55° 55° Görüyoruz ki PADC dörtge-
ni bir kirişler dörtgenidir.
2- BADC karesinin bir kirişler
dörtgeni olduğunu zaten bili-
yoruz. Yani BPADC çember-
seldir ve s(ABP)=35° dir.
P P
80°
35°
B C B C

Soru:
ABCD karesinin içerisinde alınan bir P noktası için, CP ⊥ DP, ICPI=5 br, IPDI=2 br
ise IAPI=x kaç br dir?
Çözüm:
1- AK ⊥ DP çizilirse
CPD ≅ DKA olur.
Bu durumda IPKI=3, IAKI=2 ve
|AP|=ò13 bulunur.

Soru:
ABCD karesinin [AD] ve [BC] kenarları üzerinde sırasıyla E ve F noktaları, [EF] doğru
parçası üzerinde ise bir X noktası alınıyor. AEX ve CFX üçgenlerinin çevrel çember-
leri P noktasında kesiştiğine göre, P noktasının [AC] köşegeni üzerinde olduğunu
kanıtlayınız.

Çözüm:
1- A ile P yi ve P ile C yi birleştirelim.
A E D A E D
AEXP kirişler dörtgeninde s(AEX)=α
dersek s(APX)=180°-α olur.
X X
2- [AD] // [BC] olup s(AEF)=α iken
s(CFE)=α dır.
P P
3- CFPX kirişler dörtgeni olduğu için
s(CPX)= s(CFX)=α olur. Bu sonuç-
tan sonra, s(APX)+s(CPX)=180°
B F C B F C bulunur. Bu bize A-P-C noktalarının
doğrusal olduğunu gösterir.

297