Page 304 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

5. BÖLÜM ÇOKGENLER - II

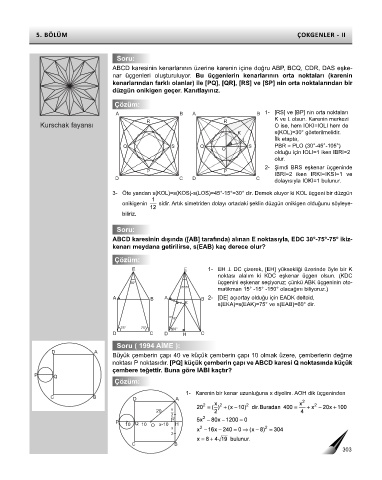
Soru:
ABCD karesinin kenarlarının üzerine karenin içine doğru ABP, BCQ, CDR, DAS eşke-
nar üçgenleri oluşturuluyor. Bu üçgenlerin kenarlarının orta noktaları (karenin
kenarlarından farklı olanlar) ile [PQ], [QR], [RS] ve [SP] nin orta noktalarından bir
düzgün onikigen geçer. Kanıtlayınız.
Çözüm:
A B A B 1- [RS] ve [BP] nin orta noktaları
K ve L olsun. Karenin merkezi
R R
Kurschak fayansı O ise, hem IOKI=IOLI hem de
K s(KOL)=30° gösterilmelidir.
1 İlk etapta,
L
Q S Q 1 S PBR ≈ PLO (30°-45°-105°)
O
olduğu için IOLI=1 iken IBRI=2
olur.
2- Şimdi BRS eşkenar üçgeninde
P P
IBRI=2 iken IRKI=IKSI=1 ve
D C D C
dolayısıyla IOKI=1 bulunur.
3- Öte yandan s(KOL)=s(KOS)-s(LOS)=45°-15°=30° dir. Demek oluyor ki KOL üçgeni bir düzgün
onikigenin sidir. Artık simetriden dolayı ortadaki şeklin düzgün onikigen olduğunu söyleye-
biliriz.

Soru:
ABCD karesinin dışında ([AB] tarafında) alınan E noktasıyla, EDC 30°-75°-75° ikiz-
kenarı meydana getirilirse, s(EAB) kaç derece olur?
Çözüm:
E E 1- EH ⊥ DC çizerek, [EH] yüksekliği üzerinde öyle bir K
noktası alalım ki KDC eşkenar üçgen olsun. (KDC
30° üçgenini eşkenar seçiyoruz; çünkü ABK üçgeninin oto-
15°15°
matikman 15° -15° -150° olacağını biliyoruz.)
A B A B 2- [DE] açıortay olduğu için EADK deltoid,
K s(EKA)=s(EAK)=75° ve s(EAB)=60° dir.
15°
15°
75° 75°
60°
D C D H C
Soru ( 1994 AİME ):
D A
Büyük çemberin çapı 40 ve küçük çemberin çapı 10 olmak üzere, çemberlerin değme
noktası P noktasıdır. [PQ] küçük çemberin çapı ve ABCD karesi Q noktasında küçük
çembere teğettir. Buna göre IABI kaçtır?
P Q
Çözüm:
1- Karenin bir kenar uzunluğuna x diyelim. AOH dik üçgeninden
C B
D A
20 x
2
P
10 Q 10 O x-10 H
x
2
C B
303