Page 309 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

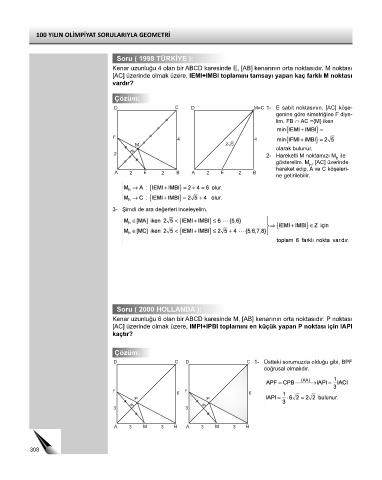
Soru ( 1998 TÜRKİYE ):
Kenar uzunluğu 4 olan bir ABCD karesinde E, [AB] kenarının orta noktasıdır. M noktası
[AC] üzerinde olmak üzere, IEMI+IMBI toplamını tamsayı yapan kaç farklı M noktası
vardır?

Çözüm:
D C D M=C 1- E sabit noktasının, [AC] köşe-
genine göre simetriğine F diye-
lim. FB ∩ AC ={M} iken
F
4 4
M 25
olarak bulunur.
2 2- Hareketli M noktamızı M ile
h
gösterelim. M , [AC] üzerinde
h
hareket edip, A ve C köşeleri-
A 2 E 2 B A 2 E 2 B
ne getirilebilir.

3- Şimdi de ara değerleri inceleyelim.

Soru ( 2000 HOLLANDA ):
Kenar uzunluğu 6 olan bir ABCD karesinde M, [AB] kenarının orta noktasıdır. P noktası
[AC] üzerinde olmak üzere, IMPI+IPBI toplamını en küçük yapan P noktası için IAPI
kaçtır?

Çözüm:
D C D C 1- Üstteki sorumuzda olduğu gibi, BPF
doğrusal olmalıdır.

F F
6 6
P P
3 3

A 3 M 3 B A 3 M 3 B

308