Page 314 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

5. BÖLÜM ÇOKGENLER - II

Soru:
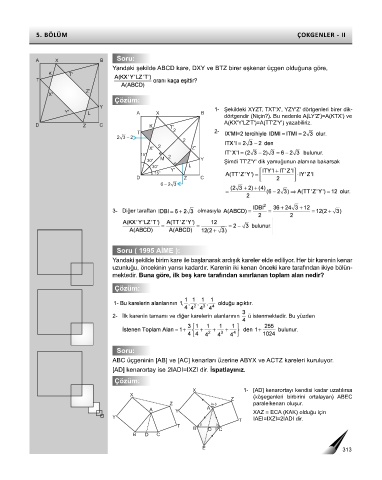
A X B
Yandaki şekilde ABCD kare, DXY ve BTZ birer eşkenar üçgen olduğuna göre,
K T'
T
Z'
X'
Çözüm:
Y
Y' L A X B 1- Şekildeki XYZT, TXT'X', YZY'Z' dörtgenleri birer dik-
dörtgendir (Niçin?). Bu nedenle A(LY'Z')=A(KTX') ve
A(KX'Y'LZ'T')=A(TT'Z'Y') yazabiliriz.
D Z C K T'
T 2 2-
23 − 2
2
2
X' Z'
15° 2
M Y
30° Şimdi TT'Z'Y' dik yamuğunun alanına bakarsak
30° L
Y'
15°
D Z C
−
62 3
3- Diğer taraftan olmasıyla

Soru ( 1995 AİME ):
Yandaki şekilde birim kare ile başlanarak ardışık kareler elde ediliyor. Her bir karenin kenar
uzunluğu, öncekinin yarısı kadardır. Karenin iki kenarı önceki kare tarafından ikiye bölün-
mektedir. Buna göre, ilk beş kare tarafından sınırlanan toplam alan nedir?
Çözüm:

2- İlk karenin tamamı ve diğer karelerin alanlarının ü istenmektedir. Bu yüzden

Soru:
ABC üçgeninin [AB] ve [AC] kenarları üzerine ABYX ve ACTZ kareleri kuruluyor.
[AD] kenarortay ise 2IADI=IXZI dir. İspatlayınız.
Çözüm:
X 1- [AD] kenarortayı kendisi kadar uzatılırsa
X (köşegenleri birbirini ortalayan) ABEC
Z
Z paralelkenarı oluşur.
A
A Y XAZ ≅ ECA (KAK) olduğu için
Y
T IAEI=IXZI=2IADI dir.
T
B D C
B D C
E 313