Page 317 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru:
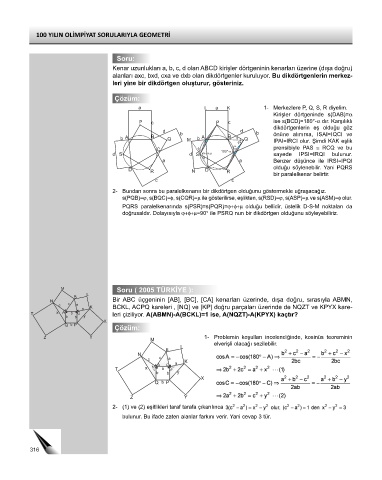
Kenar uzunlukları a, b, c, d olan ABCD kirişler dörtgeninin kenarları üzerine (dışa doğru)
alanları axc, bxd, cxa ve dxb olan dikdörtgenler kuruluyor. Bu dikdörtgenlerin merkez-
leri yine bir dikdörtgen oluşturur, gösteriniz.

Çözüm:
a L a K 1- Merkezlere P, Q, S, R diyelim.
Kirişler dörtgeninde s(DAB)=α
P c P c ise s(BCD)=180°-α dır. Karşılıklı
dikdörtgenlerin eş olduğu göz
d b d b
b A B Q M b A B Q önüne alınırsa, ISAI=IQCI ve
IPAI=IRCI olur. Şimdi KAK eşlik

C C prensibiyle PAS ≅ RCQ ve bu
d S d S 180°- sayede IPSI=IRQI bulunur.
a a Benzer düşünce ile IRSI=IPQI
D D olduğu söylenebilir. Yani PQRS
R N R
bir paralelkenar belirtir.
c c
2- Bundan sonra bu paralelkenarın bir dikdörtgen olduğunu göstermekle uğraşacağız.
s(PQB)=ϕ, s(BQC)=φ, s(CQR)=μ ile gösterilirse, eşlikten, s(RSD)=ϕ, s(ASP)=μ ve s(ASM)=φ olur.
PQRS paralelkenarında s(PSR)=s(PQR)=ϕ+φ+μ olduğu bellidir, üstelik D-S-M noktaları da
doğrusaldır. Dolayısıyla ϕ+φ+μ=90° ile PSRQ nun bir dikdörtgen olduğunu söyleyebiliriz.

Soru ( 2005 TÜRKİYE ):
M
L
B
N Bir ABC üçgeninin [AB], [BC], [CA] kenarları üzerinde, dışa doğru, sırasıyla ABMN,
c c a
a K BCKL, ACPQ kareleri , [NQ] ve [KP] doğru parçaları üzerinde de NQZT ve KPYX kare-
T x A b C leri çiziliyor. A(ABMN)-A(BCKL)=1 ise, A(NQZT)-A(KPYX) kaçtır?
b b y
X
Q b P
Çözüm:
Z Y 1- Problemin koşulları incelendiğinde, kosinüs teoreminin
M
elverişli olacağı sezilebilir.
L
B
N
c c a K
A C a
T x 180°-A b 180°-C
b b y
X
Q b P
Z Y
2- (1) ve (2) eşitlikleri taraf tarafa çıkarılınca
bulunur. Bu ifade zaten alanlar farkını verir. Yani cevap 3 tür.

316