Page 321 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

6.1 İki Çemberin Ortak Teğetleri

Bilinen birkaç tanımla başla-
yalım:
Aynı düzlemde bulunan ve iki
çembere de teğet olan doğru-
ya, bu çemberlerin ortak teğe-
ti denir. İki çemberin merkezle-
rini birleştiren doğru parçasını
kesmeyen ortak teğetlere,
ortak dış teğetler denir. İki
çemberin merkezlerini birleşti-
ren doğru parçasını kesen
ortak teğetlere, ortak iç teğet-
ler denir.
İki çemberin ortak teğetinin,
değme noktaları arasında
kalan parçasına, ortak teğet Zevkli Bir Deney:
parçası denir.
Bir üçgen ve bu üçgenin iki kenarına da
teğet olacak şekilde bir çember çizerek
başlıyoruz. Sonra farklı bir çember çiziyo-
ruz öyle ki ilk çembere ve bir başka kenar
çiftine teğet olsun. Böyle devam ederek
altıncı çembere geldiğimizde, görüyoruz
ki bu çember ilk çembere teğet olarak
a ve b sayıları için devri tamamlar. (Altı çember teoremi)
( a − ) b 2 ≥ 0
a − 2 ab + b ≥ 0
+
ab ≥ ab dir.
2
Bu özel eşitsizlik,
Aritmetik Ortalama- Soru:
Geometrik Ortalama
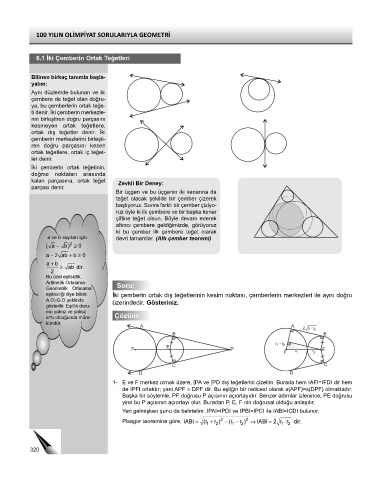
eşitsizliği diye bilinir. İki çemberin ortak dış teğetlerinin kesim noktası, çemberlerin merkezleri ile aynı doğru
A.O≥G.O şeklinde üzerindedir. Gösteriniz.
gösterilir. Eşitlik duru-
mu yalnız ve yalnız
a=b olduğunda müm- Çözüm:
kündür.
A A 2r 12 r⋅
B B
1 r − 2 r
E
F P E
F 1 r 2 r
C C
D D
1- E ve F merkez olmak üzere, [PA ve [PD dış teğetlerini çizelim. Burada hem IAFI=IFDI dir hem
de IPFI ortaktır; yani APF ≅ DPF dir. Bu eşliğin bir neticesi olarak s(APF)=s(DPF) olmaktadır.
Başka bir söylemle, PF doğrusu P açısının açıortayıdır. Benzer adımlar izlenince, PE doğrusu
yine bu P açısının açıortayı olur. Buradan P, E, F nin doğrusal olduğu anlaşılır.
Yeri gelmişken şunu da belirtelim: IPAI=IPDI ve IPBI=IPCI ile IABI=ICDI bulunur.
Pisagor teoremine göre,

320