Page 337 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

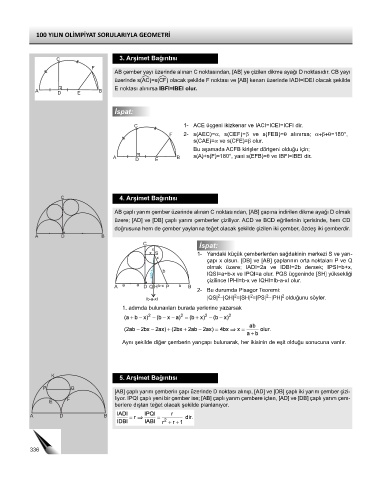
C 3. Arşimet Bağıntısı
F
AB çember yayı üzerinde alınan C noktasından, [AB] ye çizilen dikme ayağı D noktasıdır. CB yayı
ù
ù
üzerinde s(AC)=s(CF) olacak şekilde F noktası ve [AB] kenarı üzerinde IADI=IDEI olacak şekilde
E noktası alınırsa IBFI=IBEI olur.
A B
D E
İspat:
C 1- ACE üçgeni ikizkenar ve IACI=ICEI=ICFI dir.
F 2- s(AEC)=α, s(CEF)=β ve s(FEB)=θ alınırsa; α+β+θ=180°,
s(CAE)=α ve s(CFE)=β olur.
Bu aşamada ACFB kirişler dörtgeni olduğu için;
A B s(A)+s(F)=180°, yani s(EFB)=θ ve IBFI=IBEI dir.
D E

4. Arşimet Bağıntısı

AB çaplı yarım çember üzerinde alınan C noktasından, [AB] çapına indirilen dikme ayağı D olmak
üzere; [AD] ve [DB] çaplı yarım çemberler çiziliyor. ACD ve BCD eğrilerinin içerisinde, hem CD
doğrusuna hem de çember yaylarına teğet olacak şekilde çizilen iki çember, özdeş iki çemberdir.

İspat:
1- Yandaki küçük çemberlerden sağdakinin merkezi S ve yarı-
çapı x olsun. [DB] ve [AB] çaplarının orta noktaları P ve Q
olmak üzere; IADI=2a ve IDBI=2b dersek; IPSI=b+x,
IQSI=a+b-x ve IPQI=a olur. PQS üçgeninde [SH] yüksekliği
çizilince IPHI=b-x ve IQHI=Ib-a-xI olur.
2- Bu durumda Pisagor Teoremi:
2
2
2
2
2
|QS| −|QH| =|SH| =|PS| −|PH| olduğunu söyler.
1. adımda bulunanları burada yerlerine yazarsak
Aynı şekilde diğer çemberin yarıçapı bulunarak, her ikisinin de eşit olduğu sonucuna varılır.

K 5. Arşimet Bağıntısı
P Q
[AB] çaplı yarım çemberin çapı üzerinde D noktası alınıp, [AD] ve [DB] çaplı iki yarım çember çizi-
F liyor. IPQI çaplı yeni bir çember ise; [AB] çaplı yarım çembere içten, [AD] ve [DB] çaplı yarım çem-
E
berlere dıştan teğet olacak şekilde planlanıyor.
A D B

336