Page 343 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

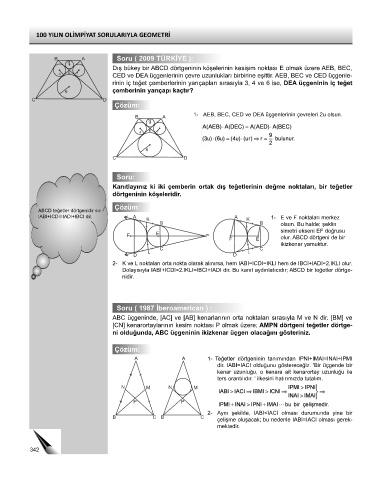
B A Soru ( 2009 TÜRKİYE ):
3
Dış bükey bir ABCD dörtgeninin köşelerinin kesişim noktası E olmak üzere AEB, BEC,
4 E r CED ve DEA üçgenlerinin çevre uzunlukları birbirine eşittir. AEB, BEC ve CED üçgenle-
rinin iç teğet çemberlerinin yarıçapları sırasıyla 3, 4 ve 6 ise, DEA üçgeninin iç teğet
6 çemberinin yarıçapı kaçtır?
C D
Çözüm:
1- AEB, BEC, CED ve DEA üçgenlerinin çevreleri 2u olsun.
B A
3
4 E r

6
C D

Soru:
Kanıtlayınız ki iki çemberin ortak dış teğetlerinin değme noktaları, bir teğetler
dörtgeninin köşeleridir.

Çözüm:
ABCD teğetler dörtgenidir ⇔
IABI+ICDI=IADI+IBCI dir. A A 1- E ve F noktaları merkez
K K
B B olsun. Bu halde; şeklin
simetri ekseni EF doğrusu
E
F P
F E olur. ABCD dörtgeni de bir
ikizkenar yamuktur.
C C
L L
D D
2- K ve L noktaları orta nokta olarak alınırsa, hem IABI=ICDI=IKLI hem de IBCI+IADI=2.IKLI olur.
Dolayısıyla IABI+ICDI=2.IKLI=IBCI+IADI dir. Bu kanıt aydınlatıcıdır; ABCD bir teğetler dörtge-
nidir.

Soru ( 1987 İberoamerican ) :
ABC üçgeninde, [AC] ve [AB] kenarlarının orta noktaları sırasıyla M ve N dir. [BM] ve
[CN] kenarortaylarının kesim noktası P olmak üzere; AMPN dörtgeni teğetler dörtge-
ni olduğunda, ABC üçgeninin ikizkenar üçgen olacağını gösteriniz.
Çözüm:
A A 1- Teğetler dörtgeninin tanımından IPNI+IMAI=INAI+IPMI
dir. IABI=IACI olduğunu göstereceğiz. 'Bir üçgende bir
kenar uzunluğu, o kenara ait kenarortay uzunluğu ile
ters orantılıdır. ' ilkesini hatırımızda tutalım.
N M N M
P P
2- Aynı şekilde, IABI<IACI olması durumunda yine bir
B C B C
çelişme oluşacak; bu nedenle IABI=IACI olması gerek-
mektedir.

342