Page 344 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

6. BÖLÜM ÇEMBERLER - II

Soru:
D c C
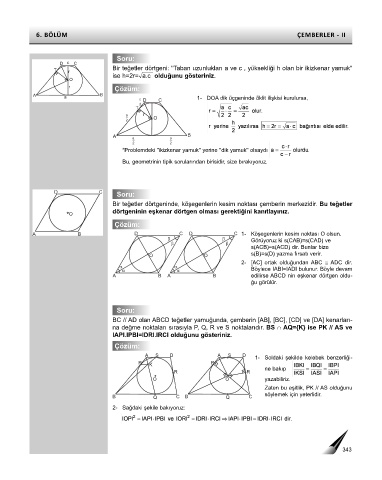
Bir teğetler dörtgeni: ''Taban uzunlukları a ve c , yüksekliği h olan bir ikizkenar yamuk''
T r
ise h=2r=óa.c olduğunu gösteriniz.
O
r Çözüm:
A B
a 1- DOA dik üçgeninde öklit ilişkisi kurulursa,
c D C
2
T
a r
O
2
A B
a a
2 2
*Problemdeki ''ikizkenar yamuk'' yerine ''dik yamuk'' olsaydı
Bu, geometrinin tipik sorularından birisidir, size bırakıyoruz.

D C Soru:
Bir teğetler dörtgeninde, köşegenlerin kesim noktası çemberin merkezidir. Bu teğetler
dörtgeninin eşkenar dörtgen olması gerektiğini kanıtlayınız.
O
Çözüm:
A B D C D C 1- Köşegenlerin kesim noktası O olsun.
Görüyoruz ki s(CAB)=s(CAD) ve

s(ACB)=s(ACD) dir. Bunlar bize
s(B)=s(D) yazma fırsatı verir.
O O
2- [AC] ortak olduğundan ABC ≅ ADC dir.

Böylece IABI=IADI bulunur. Böyle devam
A B A B edilirse ABCD nin eşkenar dörtgen oldu-
ğu görülür.

Soru:
BC // AD olan ABCD teğetler yamuğunda, çemberin [AB], [BC], [CD] ve [DA] kenarları-
na değme noktaları sırasıyla P, Q, R ve S noktalarıdır. BS ∩ AQ={K} ise PK // AS ve
IAPI.IPBI=IDRI.IRCI olduğunu gösteriniz.
Çözüm:
A S D A S D
1- Soldaki şekilde kelebek benzerliği-
P P
K
ne bakıp
R R
O O yazabiliriz.
Zaten bu eşitlik, PK // AS olduğunu
söylemek için yeterlidir.
B Q C B Q C
2- Sağdaki şekile bakıyoruz:

343