Page 362 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

6. BÖLÜM ÇEMBERLER - II

Soru:
s(C)=90° olan ABC dik üçgeninde IACI=3 ve IBCI=4 tür. Kontak üçgenin [AC] ve [AB]
kenarlarına değme noktaları sırasıyla E ve F ise, IEFI kaçtır?
Çözüm:
A A 1- İşte izlenecek yollardan biri:
2 2 BEO dik üçgeninde |BO|=ñ10
2 F 2 F
dur. BEOF kirişler dörtgeninde
1 1
O 3 O 3 Ptolemy teoremine göre;
10 3.1+3.1=|EF|.ñ10 olur.
1 1 1 1
B B
C 1 E 3 C 1 E 3
Soru ( 1991 AİME ):
E
81
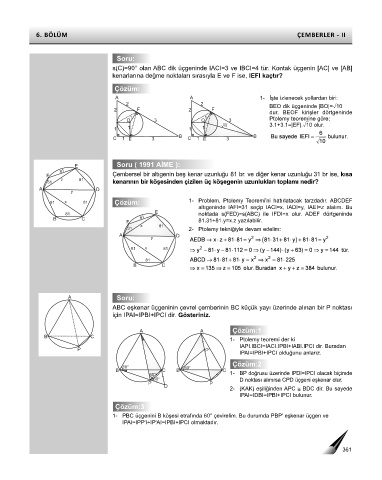
F Çembersel bir altıgenin beş kenar uzunluğu 81 br. ve diğer kenar uzunluğu 31 br ise, kısa
z 81
31 kenarının bir köşesinden çizilen üç köşegenin uzunlukları toplamı nedir?
A D
y
81 x 81 Çözüm: 1- Problem, Ptolemy Teoremi'ni hatırlatacak tarzdadır. ABCDEF
altıgeninde IAFI=31 seçip IACI=x, IADI=y, IAEI=z alalım. Bu
E
81 noktada s(FED)=s(ABC) ile IFDI=x olur. ADEF dörtgeninde
B C 81 81.31+81.y=x.z yazılabilir.
F
z 81
31 2- Ptolemy tekniğiyle devam edelim:
A D
y
81 x 81
81
B C

A Soru:
ABC eşkenar üçgeninin çevrel çemberinin BC küçük yayı üzerinde alınan bir P noktası
için IPAI=IPBI+IPCI dir. Gösteriniz.

A A Çözüm:1
B C
1- Ptolemy teoremi der ki
IAPI.IBCI=IACI.IPBI+IABI.IPCI dir. Buradan
P P'
IPAI=IPBI+IPCI olduğunu anlarız.
Çözüm:2
60° 60°
B C B C
60° 1- BP doğrusu üzerinde IPDI=IPCI olacak biçimde
60° D noktası alınırsa CPD üçgeni eşkenar olur.
P P
D
2- (KAK) eşiliğinden APC ≅ BDC dir. Bu sayede
IPAI=IDBI=IPBI+IPCI bulunur.
Çözüm:3
1- PBC üçgenini B köşesi etrafında 60° çevirelim. Bu durumda PBP' eşkenar üçgen ve
IPAI=IPP'I+IP'AI=IPBI+IPCI olmaktadır.

361