Page 371 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Çözüm:
P P P
T T A A
A
r B C
B C D
P
O
C D B
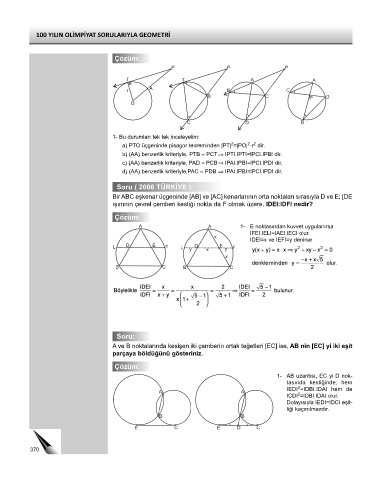
1- Bu durumları tek tek inceleyelim:
2 2
2
a) PTO üçgeninde pisagor teoreminden |PT| =|PO| -r dir.
b) (AA) benzerlik kriteriyle, PTB ≈ PCT⇒ IPTI.IPTI=IPCI.IPBI dir.
c) (AA) benzerlik kriteriyle, PAD ≈ PCB⇒ IPAI.IPBI=IPCI.IPDI dir.
d) (AA) benzerlik kriteriyle,PAC ≈ PDB ⇒ IPAI.IPBI=IPCI.IPDI dir.
Soru ( 2006 TÜRKİYE ):
Bir ABC eşkenar üçgeninde [AB] ve [AC] kenarlarının orta noktaları sırasıyla D ve E; [DE
ışınının çevrel çemberi kestiği nokta da F olmak üzere, IDEI:IDFI nedir?

Çözüm:
A A 1- E noktasından kuvvet uygulanırsa
IFEI.IELI=IAEI.IECI olur.
x
IDEI=x ve IEFI=y denirse
D E D E
L F L y x y F
x
B C B C

Soru:
A ve B noktalarında kesişen iki çemberin ortak teğetleri [EC] ise, AB nin [EC] yi iki eşit
parçaya böldüğünü gösteriniz.

Çözüm:
1- AB uzantısı, EC yi D nok-
tasında kestiğinde; hem
2
IEDI =IDBI.IDAI hem de
A A 2
ICDI =IDBI.IDAI olur.
Dolayısıyla IEDI=IDCI eşit-
liği kaçınılmazdır.
B B
E C E D C

370