Page 50 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

3. BÖLÜM ÇEMBERLER - I

Soru (2007 TÜRKİYE):
Birim çember üstünde IABI=IBCI ve s(ABC)=72° olacak şekilde A, B, C noktaları alını-
yor. BCD bir eşkenar üçgen olacak şekilde çemberin iç bölgesinde alınan bir D noktası
için, AD doğrusu çemberi ikinci kez E noktasında kesiyorsa, IDEI nedir?
Çözüm:
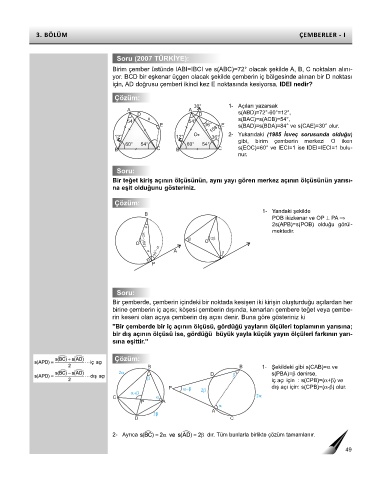
30° 1- Açıları yazarsak
A A
D D s(ABD)=72°-60°=12°,
x s(BAC)=s(ACB)=54°,
54° 54°
E 36° E s(BAD)=s(BDA)=84° ve s(CAE)=30° olur.
108°
O 2- Yukarıdaki (1985 İsveç sorusunda olduğu)
12° 12° 36°
gibi, birim çemberin merkezi O iken
60° 54° 60° 54°
B C B C s(EOC)=60° ve IECI=1 ise IDEI=IECI=1 bulu-
nur.
Soru:
Bir teğet kiriş açının ölçüsünün, aynı yayı gören merkez açının ölçüsünün yarısı-
na eşit olduğunu gösteriniz.
Çözüm:
1- Yandaki şekilde
B
POB ikizkenar ve OP ⊥ PA ⇒
2s(APB)=s(POB) olduğu görül-

mektedir.

O
O

A
P

Soru:
Bir çemberde, çemberin içindeki bir noktada kesişen iki kirişin oluşturduğu açılardan her
birine çemberin iç açısı; köşesi çemberin dışında, kenarları çembere teğet veya çembe-
rin keseni olan açıya çemberin dış açısı denir. Buna göre gösteriniz ki
''Bir çemberde bir iç açının ölçüsü, gördüğü yayların ölçüleri toplamının yarısına;
bir dış açının ölçüsü ise, gördüğü büyük yayla küçük yayın ölçüleri farkının yarı-
sına eşittir.''

Çözüm:
B B 1- Şekildeki gibi s(CAB)=α ve
D s(PBA)=β denirse,

iç açı için : s(CPB)=(α+β) ve
P dış açı için: s(CPB)=(α-β) olur.

C
P A

A

D C
2- Ayrıca dır. Tüm bunlarla birlikte çözüm tamamlanır.

49