Page 75 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru:
2
α bir reel sayı olmak üzere, sin2α=2sinαcosα ve cos2α=2cos α-1 dir. Gösteriniz.
Çözüm:
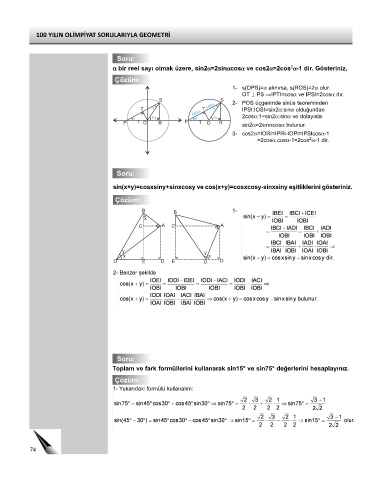
1- s(OPS)=α alınırsa, s(ROS)=2α olur.
OT ⊥ PS ⇒IPTI=cosα ve IPSI=2cosα dır.
S S 2- POS üçgeninde sinüs teoreminden
T T cos IPSI:IOSI=sin2α:sinα olduğundan
cos
2cosα:1=sin2α:sinα ve dolayısla
P 1 O R P 1 O R sin2α=2sinαcosα bulunur.
3- cos2α=IORI=IPRI-IOPI=IPSIcosα-1
2
=2cosα.cosα-1=2cos α-1 dir.

Soru:
sin(x+y)=cosxsiny+sinxcosy ve cos(x+y)=cosxcosy-sinxsiny eşitliklerini gösteriniz.

Çözüm:
B B 1-
x
C A C A

y y
x x
O E D E O D
2- Benzer şekilde

Soru:
Toplam ve fark formüllerini kullanarak sin15° ve sin75° değerlerini hesaplayınız.
Çözüm:
1- Yukarıdaki formülü kullanalım:

74