Page 76 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

3. BÖLÜM ÇEMBERLER - I

Uyarı: Soru:
90° ile 15°-30°-45°-60° ve 75° Özel üçgenlerde aşağıdaki ifadelerin doğru olduğunu gösteriniz:
nin durumu aşağıdaki şekildedir.
1) 22,5°- 67,5°-90° üçgeninde; hipotenüs, hipotenüse ait yüksekliğin 2ñ2 katına eşittir.
A
2) 22,5°- 67,5°-90° üçgeninde; 67,5° nin karşısındaki kenar uzunluğu, 22,5° nin karşısındaki
kenar uzunluğunun ñ2+1 katına eşittir.
3) 15°-75°-90° üçgeninde; 75° nin karşısındaki kenar uzunluğu, 15° nin karşısındaki kenarın
15°
uzunluğunun ñ3+2 katına eşittir.

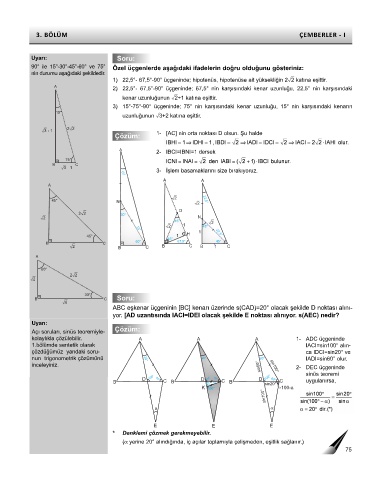
31 22 1- [AC] nin orta noktası D olsun. Şu halde
Çözüm:
A
2- IBCI=IBNI=1 dersek
75°
B C

31
3- İşlem basamaklarını size bırakıyoruz.
15°
A A
A
2
45° N 2 22,5°
D
22 30°
2 N
45° 2
2 1 45°
15°
1 22,5°
45° 1 H
45°
60° 67,5° 45°
B C
2 B C B C B 1 C
A
60°
22
2
30°
B C Soru:
6
ABC eşkenar üçgeninin [BC] kenarı üzerinde s(CAD)=20° olacak şekilde D noktası alını-
yor. [AD uzantısında IACI=IDEI olacak şekilde E noktası alınıyor. s(AEC) nedir?
Uyarı:
Çözüm:
Açı soruları, sinüs teoremiyle-
kolaylıkla çözülebilir. A A A 1- ADC üçgeninde
1.bölümde sentetik olarak IACI=sin100° alın-
çözdüğümüz yandaki soru- ca IDCI=sin20° ve
nun trigonometrik çözümünü 20° 20° 20° IADI=sin60° olur.
sin60° sin100° 2- DEC üçgeninde
inceleyiniz.
D 100° 60° D 100° 60° D 100° 60° sinüs teoremi
B C B 80° 20° C B C uygulanırsa,
80° sin20°
K 100° 100-a
sin100°

E E E
* Denklemi çözmek gerekmeyebilir.
(α yerine 20° alındığında, iç açılar toplamıyla çelişmeden, eşitlik sağlanır.)
75