Page 82 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

3. BÖLÜM ÇEMBERLER - I

Soru (2002 ÇİN):
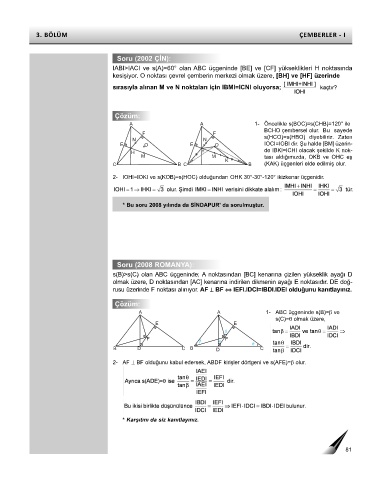
IABI>IACI ve s(A)=60° olan ABC üçgeninde [BE] ve [CF] yükseklikleri H noktasında
kesişiyor. O noktası çevrel çemberin merkezi olmak üzere, [BH] ve [HF] üzerinde
sırasıyla alınan M ve N noktaları için IBMI=ICNI oluyorsa;

Çözüm:
A A 1- Öncelikle s(BOC)=s(CHB)=120° ile
BCHO çembersel olur. Bu sayede
F F
N N s(HCO)=s(HBO) diyebiliriz. Zaten
E O E O IOCI=IOBI dir. Şu halde [BM] üzerin-
H H de IBKI=ICHI olacak şekilde K nok-
M M tası aldığımızda, OKB ve OHC eş
K
C B C B (KAK) üçgenleri elde edilmiş olur.
2- IOHI=IOKI ve s(KOB)=s(HOC) olduğundan OHK 30°-30°-120° ikizkenar üçgenidir.

* Bu soru 2008 yılında da SİNDAPUR' da sorulmuştur.

Soru (2008 ROMANYA):
s(B)>s(C) olan ABC üçgeninde; A noktasından [BC] kenarına çizilen yükseklik ayağı D
olmak üzere, D noktasından [AC] kenarına indirilen dikmenin ayağı E noktasıdır. DE doğ-
rusu üzerinde F noktası alınıyor. AF ⊥ BF ⇔ IEFI.IDCI=IBDI.IDEI olduğunu kanıtlayınız.
Çözüm:
A A 1- ABC üçgeninde s(B)=β ve
s(C)=θ olmak üzere,
E E

F F

B D C B D C
2- AF ⊥ BF olduğunu kabul edersek, ABDF kirişler dörtgeni ve s(AFE)=β olur.

* Karşıtını da siz kanıtlayınız.

81