Page 153 - ULUSAL ANTALYA MATEMATİK OLİMPİYATI 1. AŞAMA SORULARI VE ÇÖZÜMLERİ

152 Ulusal Antalya Matematik Olimpiyatları

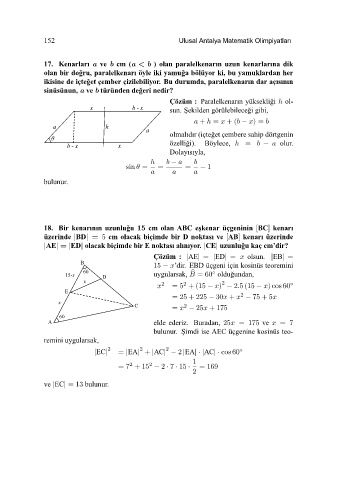
17. Kenarları a ve b cm (a<b ) olan paralelkenarın uzun kenarlarına dik
olan bir do˘ gru, paralelkenarı öyle iki yamu˘ ga bölüyor ki, bu yamuklardan her
ikisine de içte˘ get çember çizilebiliyor. Bu durumda, paralelkenarın dar açısının
sinüsünun, a ve b türünden de˘ geri nedir?
Çözüm : Paralelkenarın yüksekli˘ gi  ol­
x b - x sun. ¸Sekilden görülebilece˘ gi gibi,
 +  =  +( − )= 
a h
a olmalıdır (içte˘ get çembere sahip dörtgenin
θ
b - x x özelli˘ gi). Böylece,  =  −  olur.
Dolayısıyla,
  −  
sin  = = = − 1
  
bulunur.

18. Bir kenarının uzunlu˘ gu 15 cm olan ABC e¸skenar üçgeninin [BC] kenarı
üzerinde |BD| = 5 cm olacak biçimde bir D noktası ve [AB] kenarı üzerinde
|AE| = |ED| olacak biçimde bir E noktası alınıyor. |CE| uzunlu˘ gu kaç cm’dir?
Çözüm : |AE| = |ED| =  olsun. |EB| =
B
15 − ’dir. EBD üçgeni için kosinüs teoremini
60
15­x D uygularsak,  =60 oldu˘ gundan,
◦
b
x 2
2
 2 =5 +(15 − ) − 25(15 − ) cos 60 ◦
E
2
= 25 + 225 − 30 +  − 75 + 5
x
C =  − 25 + 175
2
60
A elde ederiz. Buradan, 25 = 175 ve  =7
bulunur. ¸Simdi ise AEC üçgenine kosinüs teo­
remini uygularsak,
2 2 2
|EC| = |EA| + |AC| − 2 |EA|·|AC|· cos 60 ◦
1
2 2
=7 +15 − 2 · 7 · 15 · =169
2
ve |EC| =13 bulunur.