Page 325 - ULUSAL ANTALYA MATEMATİK OLİMPİYATI 1. AŞAMA SORULARI VE ÇÖZÜMLERİ

324 Ulusal Antalya Matematik Olimpiyatları

Çözüm : || = || = || =  ve || =  C
diyelim. Ptolemy e¸sitli˘ ginden,
D
|||| + |||| = ||||
5 E
 || +  || =  || =  · 25 a
20
oldu˘ gundan, || + || =25 elde edilir. Di˘ ger yan­ b
dan, A
a B
4 4 || 
 ∼  oldu˘ gundan, = ;
 20
4 4 ||  − 
 ∼  oldu˘ gundan, =
 20
sa˘ glanır. Bu e¸sitlikler taraf tarafa toplanırsa,
|| + ||  25 
= veya =
 20  20
√ √
elde edilir. Buradan,  = 20 · 25 = 10 5 bulunur.

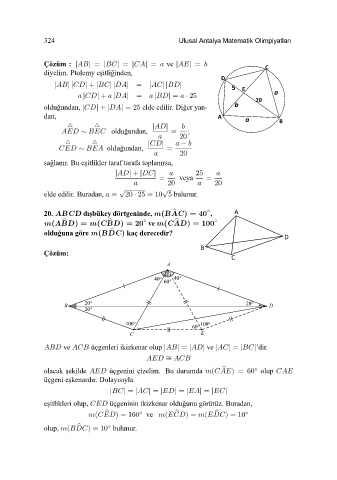
20. ABCD dı¸sbükey dörtgeninde, m(BAC)=40 , A
◦
b
◦
m(ABD)= m(CBD)= 20 ve m(CAD)=100 ◦
b
b
b
oldu˘ guna göre m(BDC) kaç derecedir?
b
D
B
Çözüm:
C

 ve  üçgenleri ikizkenar olup || = || ve || = ||’dir.
 = 
∼
olacak ¸sekilde  üçgenini çizelim. Bu durumda ()=60 olup 
◦
b
üçgeni e¸skenardır. Dolayısıyla
|| = || = || = || = ||
e¸sitlikleri olup,  üçgeninin ikizkenar oldu˘ gunu görürüz. Buradan,
◦
() = 160 ve ()= ()= 10 ◦
b
b
b
olup, ()= 10 bulunur.
◦
b