Page 329 - ULUSAL ANTALYA MATEMATİK OLİMPİYATI 1. AŞAMA SORULARI VE ÇÖZÜMLERİ

328 Ulusal Antalya Matematik Olimpiyatları

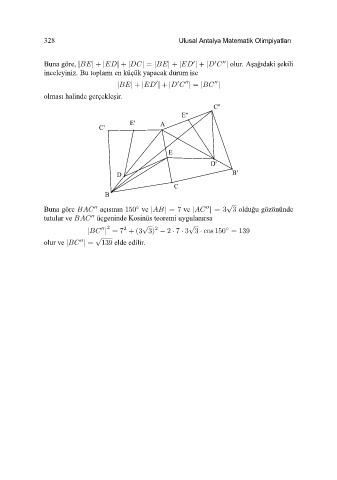
Buna göre, || + || + || = || + | | + |  | olur. A¸sa˘ gıdaki ¸sekili
00
0
0
inceleyiniz. Bu toplamı en küçük yapacak durum ise
0 0 00 00
|| + | | + |  | = | |
olması halinde gerçekle¸sir.
C''
E''
E' A
C'

E
D'
D B'
C
B
√
Buna göre  açısının 150 ve || =7 ve | | =3 3 oldu˘ gu gözönünde
00
00
◦
tutulur ve  üçgeninde Kosinüs teoremi uygulanırsa
00
√
√
00 2
2
2
◦
| | =7 +(3 3) − 2 · 7 · 3 3 · cos 150 = 139
√
olur ve | | = 139 elde edilir.
00