Page 388 - ULUSAL ANTALYA MATEMATİK OLİMPİYATI 1. AŞAMA SORULARI VE ÇÖZÜMLERİ

2019 Sınav Sorularının Çözümleri 387

Çözüm: Öncelikle  ve  de˘ gerlerini sadele¸stirelim.
µ ¶µ ¶µ ¶ µ ¶
6 12 18 180
 = ·· ·
6 6 6 6
6! 12! 18! 180!
= ···
0!6! 6!6! 12!6! 174!6!
1 1 1 180! 180!
= ··· =
6! 6! 6! 6! (6!) 30
Benzer ¸sekilde,
µ ¶µ ¶µ ¶ µ ¶
8 14 20 182
 = ···
6 6 6 6
8! 14! 20! 182!
= ···
2!6! 8!6! 14!6! 176!6!
1 1 1 182! 182!
= ··· =
2!6! 6! 6! 6! 2! (6!) 30
101 ·  101 182 · 181
olur ve = = 9191 elde edilir.
181 ·  181 2

A
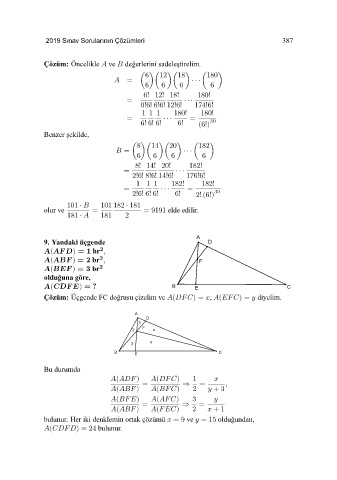
9. Yandaki üçgende D
2
A(AF D) =1 br 
2
A(ABF ) =2 br  F
A(BEF ) =3 br 2
oldu˘ guna göre,
A(CDF E) =? B E C
Çözüm: Üçgende FC do˘ grusu çizelim ve ()= , ()=  diyelim.

A
D
1
F
2 x
y
3
B E C
Bu durumda
() () 1 
= ⇒ = 
() () 2  +3
() () 3 
= ⇒ =
() () 2  +1
bulunur. Her iki denklemin ortak çözümü  =9 ve  =15 oldu˘ gundan,
()= 24 bulunur.