Page 229 - 8_sf_Dahimatik

˙
˙
˙
228 DAHIMATIK - Matematik Yarı¸smalarına Ilk Adım M.Özdemir
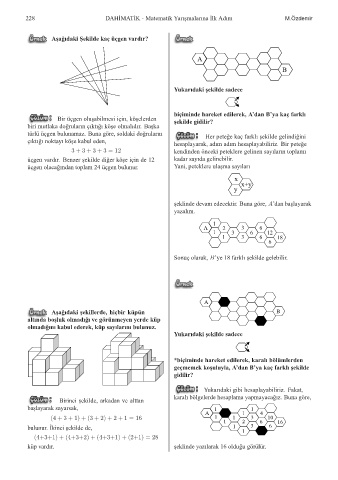
A¸sa˘ gıdaki ¸Sekilde kaç üçgen vardır?

A
B

Yukarıdaki ¸sekilde sadece

biçiminde hareket edilerek, A’dan B’ya kaç farklı
Bir üçgen olu¸sabilmesi için, kö¸selerden
¸ sekilde gidilir?
biri mutlaka do˘ gruların çıktı˘ gı kö¸se olmalıdır. Ba¸ska
türlü üçgen bulunamaz. Buna göre, soldaki do˘ gruların
Her pete˘ ge kaç farklı ¸sekilde gelindi˘ gini
çıktı˘ gı noktayı kö¸se kabul eden,
hesaplayarak, adım adım hesaplayabiliriz. Bir pete˘ ge
3 + 3 + 3 + 3 = 12 kendinden önceki peteklere gelinen sayıların toplamı
üçgen vardır. Benzer ¸sekilde di˘ ger kö¸se için de 12 kadar sayıda gelinebilir.
üçgen olaca˘ gından toplam 24 üçgen bulunur. Yani, peteklere ula¸sma sayıları
x
x+y
y

¸ seklinde devam edecektir. Buna göre, A’dan ba¸slayarak
yazalım.
1
A 2 3 6
1 3 6 12
1 3 6 18
6

Sonuç olarak, B’ye 18 farklı ¸sekilde gelebilir.

A
A¸sa˘ gıdaki ¸sekillerde, hiçbir küpün B
altında bo¸sluk olmadı˘ gı ve görünmeyen yerde küp
olmadı˘ gını kabul ederek, küp sayılarını bulunuz.
Yukarıdaki ¸sekilde sadece

*biçiminde hareket edilerek, karalı bölümlerden
geçmemek ko¸suluyla, A’dan B’ya kaç farklı ¸sekilde
gidilir?

Yukarıdaki gibi hesaplayabiliriz. Fakat,
karalı bölgelerde hesaplama yapmayaca˘ gız. Buna göre,
Birinci ¸sekilde, arkadan ve alttan
ba¸slayarak sayarsak, 1 1
A 2 1 4
(4 + 3 + 1) + (3 + 2) + 2 + 1 = 16 1 1 3 10
1 2 6 16
˙
bulunur. Ikinci ¸sekilde de, 1 3 6
1
(4+3+1) + (4+3+2) + (4+3+1) + (2+1) = 28
küp vardır. ¸ seklinde yazılarak 16 oldu˘ gu görülür.