Page 230 - 8_sf_Dahimatik

˙
˙
˙
DAHIMATIK - Matematik Yarı¸smalarına Ilk Adım 229

B
A
A
C B

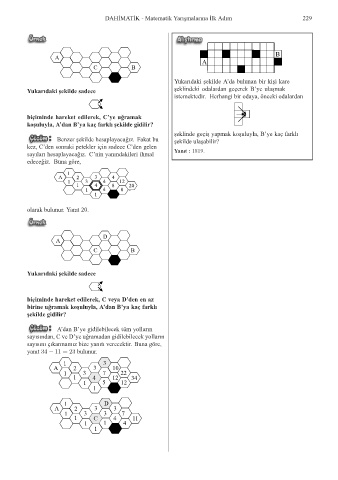
Yukarıdaki ¸sekilde A’da bulunan bir ki¸si kare
¸ seklindeki odalardan geçerek B’ye ula¸smak
Yukarıdaki ¸sekilde sadece
istemektedir. Herhangi bir odaya, önceki odalardan

biçiminde hareket edilerek, C’ye u˘ gramak
ko¸suluyla, A’dan B’ya kaç farklı ¸sekilde gidilir?
¸ seklinde geçi¸s yapmak ko¸suluyla, B’ye kaç farklı
Benzer ¸sekilde hesaplayaca˘ gız. Fakat bu ¸ sekilde ula¸sabilir?
kez, C’den sonraki petekler için sadece C’den gelen
Yanıt : 1819.
sayıları hesaplayaca˘ gız. C’nin yanındakileri ihmal
edece˘ giz. Buna göre,
1
A 2 3 4
1 3 4 12
1 4 8 20
1 4 8 6
1
olarak bulunur. Yanıt 20.

D
A
C B

Yukarıdaki ¸sekilde sadece

biçiminde hareket edilerek, C veya D’den en az
birine u˘ gramak ko¸suluyla, A’dan B’ya kaç farklı
¸ sekilde gidilir?

A’dan B’ye gidilebilecek tüm yolların
sayısından, C ve D’ye u˘ gramadan gidilebilecek yolların
sayısını çıkarmamız bize yanıtı verecektir. Buna göre,
yanıt 34 11 = 23 bulunur.
1 3
A 2 3 10
1 3 7 22
1 4 12 34
1 5 12
1

1 D
A 2 3 3
1 3 3 7
1 C 4 11
1 1 4
1