Page 365 - 8_sf_Dahimatik

˙
˙
˙
364 DAHIMATIK - Matematik Yarı¸smalarına Ilk Adım M.Özdemir
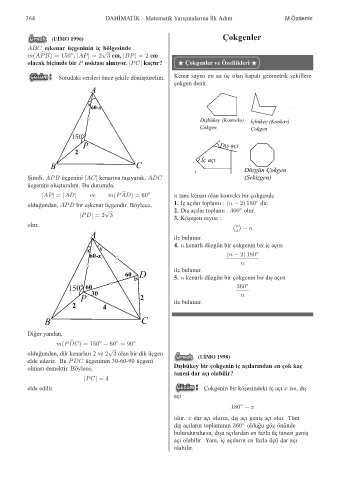
(U ˙ IMO 1996) Çokgenler
ABC e¸skenar üçgeninin iç bölgesinde
p
m(APB) = 150 ; jAPj = 2 3 cm, jBPj = 2 cm

b
olacak biçimde bir P noktası alınıyor. jPCj kaçtır? F Çokgenler ve Özellikleri F

Sorudaki verileri önce ¸sekile dönü¸stürelim. Kenar sayısı en az üç olan kapalı geometrik ¸sekillere
çokgen denir.
A
x
60-x

Dışbükey (Konveks) İçbükey (Konkav)
Çokgen Çokgen
o
150
P Dış açı
2
İç açı
B C
) Düzgün Çokgen
¸ Simdi, APB üçgenini [AC] kenarına ta¸sıyarak, ADC (Sekizgen)
üçgenini olu¸sturalım. Bu durumda,

b
jAPj = jADj ve m(PAD) = 60 n tane kenarı olan konveks bir çokgende
˙

oldu˘ gundan, APD bir e¸skenar üçgendir. Böylece, 1. Iç açılar toplamı : (n 2) 180 dir.

p 2. Dı¸s açılar toplamı : 360 olur.
jPDj = 2 3
3. Kö¸segen sayısı :
olur. n
n
2
A ile bulunur.
4. n kenarlı düzgün bir çokgenin bir iç açısı
x x
60-x (n 2) 180
n
ile bulunur.
60 D 5. n kenarlı düzgün bir çokgenin bir dı¸s açısı
150 o 60 360
30 n
P 2 ile bulunur.
2 4
B C

Di˘ ger yandan,
m(PDC) = 150 60 = 90

b
p
oldu˘ gundan, dik kenarları 2 ve 2 3 olan bir dik üçgen
(U ˙ IMO 1998)
elde ederiz. Bu PDC üçgeninin 30-60-90 üçgeni
olması demektir. Böylece, Dı¸sbükey bir çokgenin iç açılarından en çok kaç
tanesi dar açı olabilir?
jPCj = 4
elde edilir. Çokgenin bir kö¸sesindeki iç açı x ise, dı¸s
açı

180 x
olur. x dar açı olursa, dı¸s açı geni¸s açı olur. Tüm
dı¸s açıların toplamının 360 oldu˘ gu göz önünde

bulundurulursa, dı¸sa açılardan en fazla üç tanesi geni¸s
açı olabilir. Yani, iç açıların en fazla üçü dar açı
olabilir.