Page 367 - 8_sf_Dahimatik

˙
˙
˙
366 DAHIMATIK - Matematik Yarı¸smalarına Ilk Adım M.Özdemir
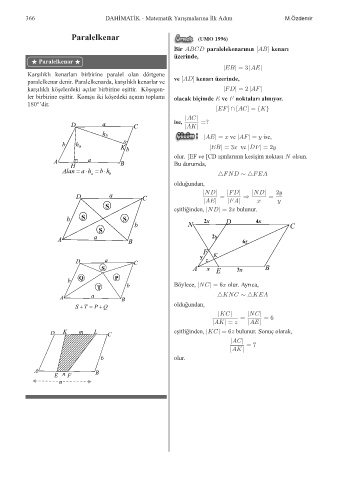
Paralelkenar (UMO 1996)
Bir ABCD paralelekenarının [AB] kenarı
üzerinde,
F Paralelkenar F

jEBj = 3 jAEj
Kar¸sılıklı kenarları birbirine paralel olan dörtgene
ve [AD] kenarı üzerinde,
paralelkenar denir. Paralelkenarda, kar¸sılıklı kenarlar ve
kar¸sılıklı kö¸selerdeki açılar birbirine e¸sittir. Kö¸segen- jFDj = 2 jAFj
ler birbirine e¸sittir. Kom¸su iki kö¸sedeki açının toplamı olacak biçimde E ve F noktaları alınıyor.

180 ’dir.
[EF] \ [AC] = fKg
jACj
D a C ise, jAKj =?

h b
jAEj = x ve jAFj = y ise,
b h a
K b jEBj = 3x ve jDFj = 2y
olur. [EF ve [CD ı¸sınlarının kesi¸sim noktası N olsun.
A a B Bu durumda,
H

Alan  a h  b h

a b 4FND 4FEA
oldu˘ gundan,
D a C jNDj = jFDj ) jNDj = 2y
jAEj jFAj x y
S
e¸sitli˘ ginden, jNDj = 2x bulunur.
b S S 2x D 4x
b N C
S
A a B 2y 6z

F
y K
D a C z
S A x E 3x B
Q P
b
T b Böylece, jNCj = 6x olur. Ayrıca,
A a B 4KNC 4KEA
oldu˘ gundan,
S T  P Q


jKCj jNCj
= = 6
jAKj = z jAEj
D K m L C e¸sitli˘ ginden, jKCj = 6z bulunur. Sonuç olarak,
jACj
= 7
jAKj
b olur.
A B
E n F
a